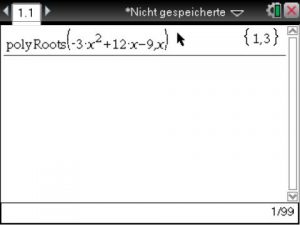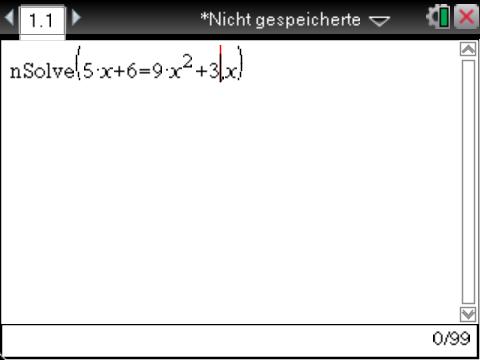
In diesem Artikel werde ich erklären, wie man mit dem TI nSpire CX eine quadratische Gleichung lösen kann.
Mit der beschriebenen Methode lassen sich ebenso weitere polynomiale Gleichungen lösen bis zu 30. Grades lösen.
Was ist eine polynomial Gleichung? Falls der Begriff unklar sein sollte findet sich hier eine Erklärung.
Um eine quadratische Gleichung zu lösen muss man sich ersteinmal im Calculator oder Scratchpad Modus befinden.
Anschließned wählt man:
Code: <Menü> – <3> [Algebra] – <3> [Polynomwerkzeuge] – <1> [Wurzeln eines Polynoms finden…]
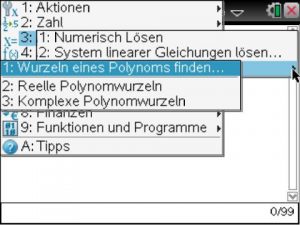
Anschließend erscheint ein Pop-Up Fenster, in welchem man den Grad einstellen kann. Hierbei handelt es sich um den größten Exponenten in der polynomial Gleichung. Da meist eine quadratische Gleichung zu lösen ist, ist der Wert 2 voreingestellt. Dieser lässt sich jedoch über eine manuelle Eingabe oder die Pfeilbuttons neben dem Eingabefeld ändern.
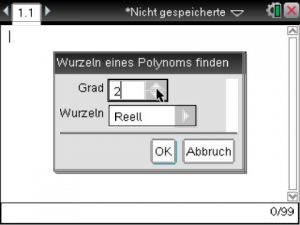
Es erfordert noch eine weitere Eingabe, und zwar die der “Wurzeln”, bevor man die Gleichung eingeben kann. Hierbei wird die meiste Zeit über vermutlich der Modus Reell der richtige sein, das heißt, es gibt keine Wurzeln aus negativen Zahlen. Falls dies doch gewünscht ist, kann man den Modus auch auf Komplex ändern, was in der Regel allerdings nicht der Fall ist.
Mit einem Klick auf OK öffnet sich erneut ein Pop-Up, in welches wir die Werte der Koeffizienten (=Vorfaktoren) der einzelnen Teile unserer polynomial Gleichung eingeben müssen. Kommt ein Teil nicht vor, so gibt man eine Null ein.
Exemplarisch führe ich dies am Beispiel der Funktion [latex] f(x)=-3x^2+12x-9 [/latex] durch.
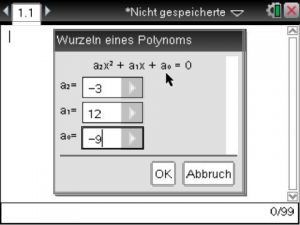
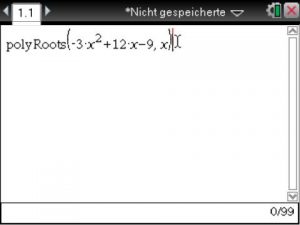
Anschließend genügt noch ein Klick auf <enter> und die Berechnung erfolgt.